Unit three blog reflection

In this unit I learned about:

• ·      Newton’s third law of motion
•     Action reaction pairs
•     Adding non-parallel vectors
•      Universal gravitational force
•     Tides
•     Momentum and impulse relationship
•     Conservation of momentum

Newton’s third law of motion states that whenever one object exerts a force on a second object, the second object exerts an equal and opposite force on the first. Take a car for example; the tires of a car push against the road while the road pushes back on the tires, the road interact with an equal and opposite force. 

One of the harder questions that helped me understand newtons third law and action reaction pairs was why a horse pulls a buggy. 

Buggy pushes earth forward. Earth pushes buggy backward.

Horse pushes ground backward. Ground pushes horse forward.

Horse pulls buggy forward. Buggy pulls horse backward.

The horse pulls the buggy with the same force as the buggy pulls on the horse. This is because of newtons 3rd law that states with every action there is an equal and opposite reaction. The reason why the horse is able to pull the buggy is because it is able to push on the ground harder than the buggy.

Adding non-parallel vectors

The F net up and F weight down are equal and opposite (action reaction pair).

Universal gravitational force:

Everything with mass attracts all other things with mass.

Force depends on

1. Mass of objects F ~ m
2. Distance between the objects
1. farther apart = less force on the 2 objects, F~1/d (inversely proportional) 

Inverse square law: 

farther away you get it will be one over the distance squared. F~ 1/d^2 (force is inversely proportional to the distance squared). To see this in an real life example, a man standing on a mountain is farther away from the center of the universe than a man standing on sea level, therefore the man on the mountain is experiencing less of a gravitational pull towards the earth than that of the other man.

Universal gravitational formula:

The purpose of G is to make the force into newtons. G = 7 * 10^-11 Nm^2/kg^2

An example problem for using this equation is; find the force between the moon and the earth. The earths mass is 6 *10^24 and the moons mass is 7 * 10^22, the distance is 4 * 10^8. The first step is the separate the equation like this.

After solving the equation the answer should be 18.4 * 10^19 N.

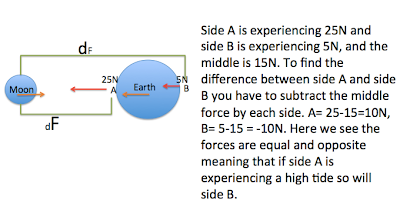
Tides was the topic that I found most difficult in this unit, because the idea that the forces between the moon and earth were equal on opposite sides of the earth was confusing. I overcame this difficulty by watching video's on youtube and searching on google for different explanations on the topic. What eventually made the lightbulb click was the understanding that tides are not caused by just the force between the moon and earth, but that they are caused by the difference in force on each side of the earth. 

There are two types of tides, and they are spring tides and neap tides. This is what they look like: 

Tides are caused by the difference in force felt by opposite sides of the earth. Tides change every 6 hours, therefore in a day there are 2 high tides and 2 low tides.

Momentum and impulse relationship

Equation for momentum: p=mv (mass times velocity)

Change in momentum equals the final momentum minus the initial momentum: ∆p= p final - p initial

• The change in momentum is the same regardless of if you stop quickly or slowly

Impulse is the force upon something multiplied by the time that the force is applied: J=F∆t

Impulse is equal to the change in momentum:  J=∆p

A question that helped me understand this concept was; why do bun-jee jumpers use elastic cords rather than metal?

In answering this question first establish that the jumper will go from moving to non moving no matter how they are stopped therefore, the change in momentum (∆p) is the same

p=mv

∆p=p final - p initial 

Since the change in momentum is the same regardless of how the egg is stopped, the impulse is also going to be the same regardless of how quickly it is stopped

∆p=J

Bun-jee jumpers use elastic cords because it stops them over a longer period of time, since the impulse is constant the force on them is small. Smaller force on the jumper means lower chances of injury.

J= F∆t (metal cord)          J= F∆t (elastic cord)

Conservation of momentum;

 

Because of newtons third law which states that forces are equal and opposite we can prove that the two balls rolling towards each other regardless of their mass and speed will experience the same amount of force. Moreover their will be no net change in momentum after the collision.

FA=-FB

FA∆t = -FB∆B

JA = -JB

 ∆pA = -∆pB

The momentum of each ball changes in a way in which the sum momentum of each ball is zero. The momentum of the balls before they hit is p total before = p total after.

The two types of collisions are elastic collisions (when the objects bounce off of one another) and an inelastic collisions (when objects collide and don't bounce away).

Elastic collision:

p total before = p total after

mAvA + mBvB =  mAvA + mBvB

Inelastic collision:

p total before =  p total after

mAvA + mBvB = m A+B(vAB)

But what if ball A hits ball B not straight on? why would both of the balls move?

They both move because momentum in the y-axis is consered. Ball A does not stop because there needs to be a zero net momentum to cancel out the y momentum of the second ball

My effort was mainly focussed towards class and homework problems because it is where I can actively learn by asking questions, and solve problems. My confidence in physics is slowly growing, and the more we learn in class the more I am able to relate class discussions to my everyday life. My approach to solving difficult problems is to first try and solve it by myself using my notes, then if that doesn't help I usually ask my teacher or a classmate. Collaboration with group members is definitely an aspect of class that I need to work on, usually it is hard to find time for all of us to work together and create an equal balance of work on group projects. My goal for next unit is to not get behind on my studies, when taking a quiz on a new topic I don't want to be questioning myself on wether or not I have fully understood the previous topic we had learned.

A connection that I made between what we have studied to everyday life is that while go carting with my brothers, when one of them hits me we both experience the same force. Therefore whenever my brother crashes into me i'm also technically crashing into him. 

Here is my podcast video on the horse and buggy question stated earlier, hope you enjoy! 

What Are Tides?

This website offers a easy to follow animation of the moon revolving around the Earth and how this effects whether or not one part of the Earth is experiencing a spring or neap tide. This website also gives a clear description of the different strength levels on the Earths gravitational pulls. The animation of the tidal bulge illustrates how the gravity "stretches" the water towards the moon.
http://www.mmscrusaders.com/newscirocks/tides/tideanim.htm

Unit two reflection

The first thing we learned about in this unit was Newton’s second law, which is:

 a=fnet/m  which translates to acceleration = net force divided by mass

From this equation we can conclude that acceleration is directly proportional to net force (a~fnet)

·      As acceleration increases net force will also increase

·      As acceleration decreases net force will also decrease

We can also conclude that acceleration is inversely proportional to mass (a~1/m)

·      As mass increases acceleration decreases

·      As mass decreases acceleration increases

Another part of Newton’s second law is w=mg (weight is equal to mass multiplied by gravity)

Here is an example equation:

A 2kg cart is being pulled by a 3kg hanger

1. What is the mass of the system? The mass is the mass of the cart and the hanger added together, and the answer is 5 kg
2.  What is the force on the system? Use the equation w=mg to change the mass of the hanger from kg into newton’s. (5)(10)=50 newton’s is the force on the system
3. What is the acceleration of the system? The equation used to solve for acceleration is a= fnet/mass and you should get 10m/s^2 = 50N/5kg

In the lab we conducted in class we created a data set of the acceleration of a cart while increasing the mass and keeping the force(N) constant. Our data showed that as the mass of the cart increased the acceleration decreased. When we graphed our results we put mass on the x-axis and the net force on the y-axis. We then compared this to the equation of the line (y=mx+b) and realized that it was the same as Newton’s second law a= (1/m)(fnet) and 1/m is equal to the slope of the line. In the second part of our experiment we changed the force and kept the mass of the system constant. We concluded that as we increased the net force of the system the acceleration of it increased. My group the plugged this into the equation of a line and got: a= (fnet)(1/m) where the net force is equal to the slope

The second concept we learned about was skydiving

Speed is directly proportional to air resistance

·      As speed increases, the force of air resistance increase as well

·      As speed decreases, the force of air resistance decreases as well

Lest say the person skydiving has a  fweight of 20kg therefore in order to find the acceleration of this person you first have to find the fnet by subtracting the persons weight by the air resistance. do w=mg  and get 200N this is the net force of the person. 

As they are falling (before opening their parachute):

• Their velocity is increasing, and their acceleration and net force are decreasing. This is because their air resistance in increasing causing the net force to decrease
•  Eventually after traveling for a certain about on time the person will reach terminal velocity
• Terminal Velocity: Constant speed of a freely falling object, which occurs when the air resistance is equal to the f weight.
• At terminal velocity the persons acceleration and net force are both at zero

As they open their parachute

• When they open the parachute the acceleration increases in the opposite direction because it is not longer moving at a constant speed.
• When speed and air resistance are in the opposite direction they are slowing down. Eventually the person will reach a new terminal velocity but this one will have a slower velocity.
• But how does the acceleration, net force, force of air resistance, and velocity compare to the original terminal velocity?
• Acceleration at both terminal velocities will be at zero
• Net force (fweight - fair) will be the same at both velocities because the fweight always remains constant.
• Force of air resistance is the same at both terminal velocities because at terminal velocity the force of air resistance is equal to the weight and since the weight remains constant, the force of air resistance will also be the same at both velocities.
• The Velocity will be slower at the second terminal velocity because there is more surface area.

If a ball is thrown straight upwards at 40m/s then this means at t=0 the ball is moving at 40m/s

t=0  -- v=40m/s

t=1 -- v=30m/s

t=2 -- v=20m/s

t=3 -- v=10m/s

t=4 -- v=0m/s

t=5 -- v=10m/s

t=5 -- v=20m/s

t=6 -- v=30m/s

t=7 -- v=40m/s

t=8 -- the ball will be on the ground

Here we can conclude that the ball was in the air for a total of 8 seconds, and that the velocity of the ball at the top of it's path was 0m/s. In order to find out how hight the ball was at the top of its path we use the equation d=1/2(g)(t)^2, the equation should look like d=1/2(10)(4) = 20 meters. 

        

The path one takes when jumping off a cliff is called a parabolic path (makes a parabola on a graph)
Example problem: If a plane drops a package from 130 meters in the air while moving 90 m/s in the horizontal direction then we can find out the following (side note: the horizontal velocity remains the same throughout the fall):

• How long is the package in the air for before hitting the ground?
• Since we already know how hight the package is we plug in the vertical distance into the equation d=1/2(g)(t)^2. 130 = 1/2 (10)(t)^2
• 130=5t^2
• 26=t^2
• 5=t
• How far away is the package from the area it was dropped (horizontal distance) ?
• We use the equation v=d/t, since we already know the velocity of the plane in the horizontal direction (90m/s) and the time the box spent in the air we can multiply the two to solve for the horizontal distance. 90=d/5. d=18 meters
• How fast was the package moving at 3 seconds?
• v=gt, (10)(3)= 30m/s

Another major topic we learned about in this unit was throwing things up at an angle
In this unit we learned how to solve for how fast something was moving while being thrown up at an 45 degree angle. For example, if a ball was thrown up with a vertical velocity of 20m/s and had a horizontal velocity of 30m/s then we can use this to calculate the initial velocity of the ball using the equation
 a^2 +b^2 =  c^2, and by plugging in the velocities for a and b you should get:
400+900=c^2
1300=c^2
36=c
When trying to solve for how far the ball travels use the equation v=d/t.
A the top of the balls path the ball will be moving 0m/s in the vertical direction and 30m/s in the horizontal direction.

• What I found to be most difficult in this unit was understanding falling through the air. I overcame this difficulty by spending more time doing practice problems and searching online for other explanation on how falling through the air works. What really made my lightbulb click was understanding that when acceleration and velocity are in the opposite direction then the object is changing speed. Another breakthrough I had was understanding the the more surface area an object has the greater air resistance it will have causing it to have a slower velocity.
• I find that I am very persistent in my work, for when I don't understand a topic I make a conscious effort to ask people for explanations or sometimes I even go into conference period to ask questions. I do this because I know that if I don's master these skills now, then I will struggle even more in the units to come.
• My goals for this next unit is to spend more time looking over my notes from class and podcast video so that by the time we take quizzes I will be ready.
• I find that I can apply throwing things up at an angle to tennis, for before I never really thought about the projectile motion of the ball after I hit it. And I never took into account that it actually mattered how fast the ball moves in the vertical direction and the horizontal direction determines if the ball will go in.

Here is my podcast video about throwing things up at an angle, hope you enjoy!

Free Falling

This is a free fall video/song that I found on youtube that I thought gave a good summary of aspect free fall. First of all free fall is when an object falls due to the effect of gravity only, and under the influence of gravity there is no air resistance. In a free fall equation acceleration is equal to gravity (a=g) this is because the object is always accelerating at a constant rate of 10m/s.
How to calculate an objects velocity in free fall: v=gt (velocity is equal to gravity multiplied by time)
How to calculate how far an object has traveled in a time span: d=1/2(g)(t)^2 (distance equals half of gravity multiplied by the time squared)
An important concept to understand about free fall is that weight does not matter.