Unit 4 Reflection

In this unit I learned about:

1. Rotational and Tangential velocity
2. Rotational inertia
3. Conservation of angular momentum
4. Torque
5. Center of mass/gravity
6. Centripetal/Centrifugal force

Rotational velocity (angular speed) is the number of rotations or revolutions per unit of time. For example all parts of a marry go round share the same rotational velocity because they go around the axis of ration the same number of times.

Tangential velocity (linear speed) is greater on the outer edge of a rotating object than it is closer to the axis of rotation. For example a person siting closer to the edge of the merry go round is traveling a farther distance in the same amount of time as someone sitting closer to the axis of rations; therefore, they have a greater tangential velocity.

Rotational inertia is the property of an object to resist change in its rotational state. Rotational inertia depends on the distribution of mass, for the greater the distance the mass is from the axis of rotation the more rotational inertia there will be. For example an ice skater spinning around in one place with their arm spread will have more rotational inertia than an ice skater spinning with their arm drawn in towards their chest. As a result of less rotational inertia the skater has a greater rotational velocity.

Conservation of angular momentum states that in a system with no external force the momentum before and after a reaction are equal. The equation we used to solve for this is:  

rotational inertia (before) x rotational velocity (before) = rotational inertia (after) x rotational velocity (after).

Torque causes rotation. It is the product of a lever arm and the force that produces the rotation; 

torque = lever arm x force. Three ways to increase the torque on something is by increasing the lever arm, increase the force, or do both. Take a door for example, the door knob is place farthest away from the axis of ration because that way when there is a longer lever arm there is less force need to create a torque. If the door knob was placed closer to the hinges then it would require more force to close the door because there is a shorter lever arm.

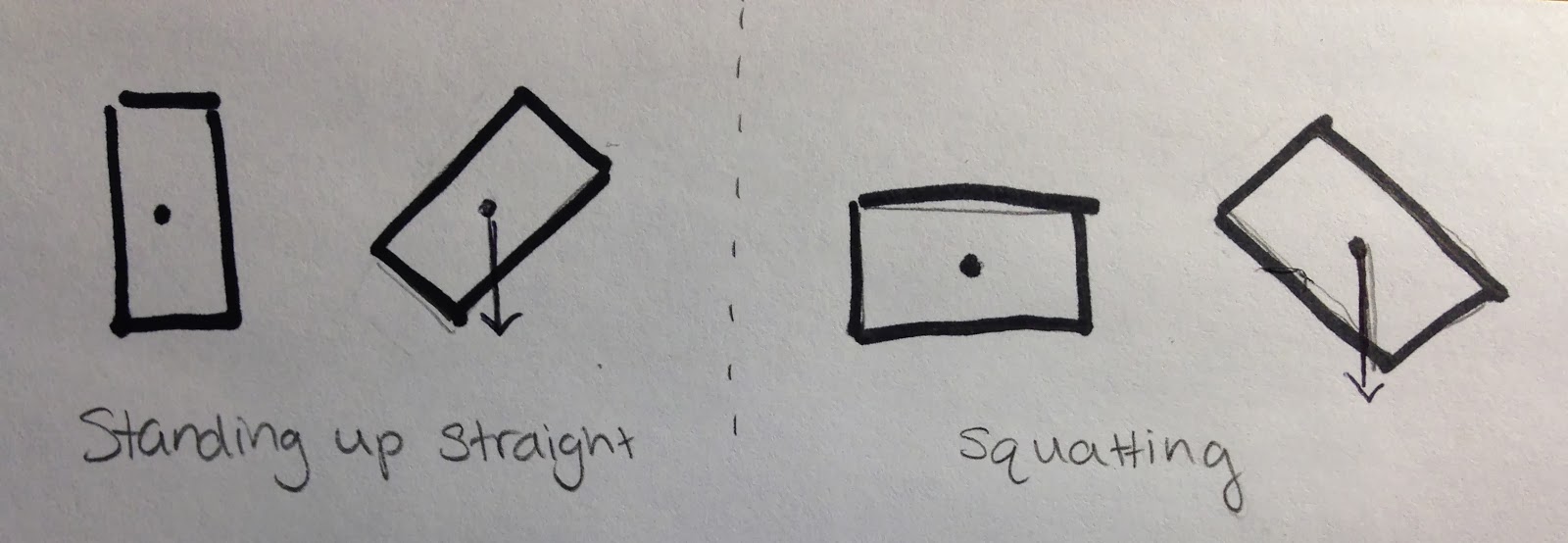
Center of mass/gravity is the average position of an objects mass. One of the main questions involving center of mass is why do do wrestlers spread their legs apart and squat over? When they widen their stance their base of support is also wider meaning that more force will be need to push them until their center of mass is not over their base of support. Wrestlers also bend their legs because it lowers their bas of support, making it harder for the opponent to knock them over. This example is illustrated in the drawing below.

Centripetal/Centrifugal force. Centripetal force is a center seeking force that draws a body towards the center. For example when a car rounds a corner the friction between the tires and the road provides the centripetal force that keeps the car on the curved road. Centrifugal force is the apparent outward force on a rotating or revolving body. Pretend that you are in the car that is rounding the corning, when car first begins to turn you hit the side of the car door (door on the opposite side of the center of curvature). This is what we call the centrifugal force, it is not a real force but rather a feeling we have, for in actuality we hit the side door because we were once going straight and now being forced to turn in a different direction. This can be related to newtons 3rd law because you push out against the door, only because the door pushes you in. An illustration for this example is shown below.

What was most difficult for me in this unit was understanding the question about why train wheels are shaped the way they are, and how they stay on track. The correct answer to such a question is; because the wheels are connected by a shaft, their rotational speed must be the same, but when one wheel has a larger radius, that side has a greater linear velocity causing the train to curve in towards the center of the track.

I overcame this difficulty by talking the problem step by step with my teacher and asked questions concerning the difference between rotational and tangential velocity. What ultimately made the lightbulb click was understanding that every position on the wheels (small and big) are experiencing the same rotational velocity, and that the reason they stay on track is because the wheel with the larger part on the track is covering a greater distance than the part with the smaller radius on the track. This allows the wheels to balance out.

I worked hard when studying for quizzes and when searching for resources for my blog, and I hope that it will pay off when I take the unit test. My goal for next unit is to try and make longer blog descriptions whenever I post a link, for I think it will be beneficial to my viewers and myself. A connection from this unit that I made to everyday life is that whenever i'm on a roller coaster that goes upside down, the people don't fall out because the centripetal force isn't as strong as the velocity in which it travels at. 

A couple of my classmates and I created a podcast video discussing the definition of torque. Creating this video really helped me understand torque and I hope it does the same for you, enjoy!

Finding the Mass of a Meter Stick without using a Scale

In part a of step 1 the meter stick is not balanced on the edge of the table; therefore, it has a torque. Here is a picture of what it looked like.

In part b of step 1 the meter stick is balanced on the edge of the table. When the center of gravity is on top of the table there is no lever arm meaning that there will be no torque (note. The line in the middle of the meter stick is the center of gravity).

In part c of step 1, 100g (mass) is added to the end of the stick and when it is balanced there is no lever arm, but the center of gravity of the system is different than the center of gravity of the meter stick by itself.

Step 2 of solving for the mass of the meter stick was planning out what equations we needed and what measurements we needed to plug into these equations. My partner and I concluded that we would need to use the equation w=mg to convert mass to weight and vise versa. The other equation we needed to use was torque= force x lever arm. The measurements we got was the lever arm of the clockwise torque which was 22.7 meters and the counter clockwise lever arm which was 28 meters. 

Step 3 we tried out our plan, and this is what it looked like:

First my partner converted 100g to .10 kg to put in the equation w=mg, this way we could find the force acting on the system in the clockwise direction. Since we already measured the lever arm in the clockwise direction we were able to find the torque of it using the equation torque= (.98)(22.7) and we got 22.25N. Then we knew that to find the lever arm of the counter clockwise direction we had to measure from the center of gravity of the system to the center of gravity of the meter stick which was 28cm. By using the equation counter clockwise torque = clockwise torque we were able to solve algebraically for the force which is equal to the mass of the stick. Our answer to the equation was that the stick weighed 81g, and when we weighed it on the scale we found that we were only .01g off our estimate. 

Torque and Center of Mass

Torque:
 http://www.physics.uoguelph.ca/tutorials/torque/Q.torque.intro.html

Center of Mass:
http://dev.physicslab.org/Document.aspx?doctype=3&filename=RotaryMotion_CenterMass.xml

The first website addresses the definition of what torque is and how we measure it. The second website explains in detail the definition of the center of mass, and even gives similar examples that I did in class.
Torque is the measure of how much a force acting on a object causes it to rotate. The equation we learned to find out the torque of something is, torque = force x lever arm (lever arm is the distance from the axis of rotation). For example when you push a door closed you don't have to apply a lot of force due to the fact that you are farther away from the axis of rotation. If you were to push the door closed closer to the hinges, you would have to push with a greater force because the lever arm is smaller.
The center of mass is the point representing the average position of the matter in a body or a system. When a object is perfectly balanced we know its center of mass is over its base, because if it wasn't then the object would tip over. Systematically speaking, when the center of mass is not over the base of an object it creates a lever arm which means a force will cause the object to rotate on it's axis.

Angular Momentum

In class we recently learned about angular or rotational momentum, but before we learned about this we had to understand what rotational inertia was. Rotational inertia is the property of an object to resist changes in a spin, the more mass an object has the more rotational inertia it has (mass~rotational inertia). The rotational inertia also depends on the placement of the mass, for example a basketball has more mass on the outside which is farther away from the balls axis which is in the center because of the this the balls rotational inertia is greater than a ball with mass closer to its axis. When the students are squatting down farther from the center of the spinning wheel on the playground the system has more rotational inertia, but when to students stand up and move towards the center they begin to speed up because they are moving closer to the axis which means there is less rotational inertia.The conservations of rotational momentum takes place when the total momentum before they sped up equals the total momentum as the students are moving faster. The equation we learned for this was rotational momentum is equal to rotational inertia x rotational velocity.